Series convergence divergence flow chart – Introducing the Series Convergence/Divergence Flow Chart, a groundbreaking tool that empowers you to navigate the intricacies of series convergence and divergence. This comprehensive guide unravels the complexities of series, providing a clear and systematic approach to understanding their behavior.
Embark on a journey through the fascinating world of series convergence/divergence, where we delve into real-world applications, common pitfalls, and advanced concepts, ensuring a thorough understanding of this fundamental mathematical concept.
1. Introduction to Series Convergence/Divergence: Series Convergence Divergence Flow Chart
Series convergence and divergence are fundamental concepts in mathematics that determine the behavior of infinite series. A series is a sum of an infinite number of terms, and its convergence or divergence refers to whether the sum approaches a finite value or not.
Understanding series convergence is crucial for various reasons. It allows us to determine whether a given series has a meaningful sum, which is essential in calculus, physics, and engineering. Additionally, it helps us analyze the behavior of functions represented by power series and Fourier series.
Examples of convergent series include geometric series and alternating harmonic series, while examples of divergent series include harmonic series and p-series with p ≤ 1.
2. Flowchart for Series Convergence/Divergence
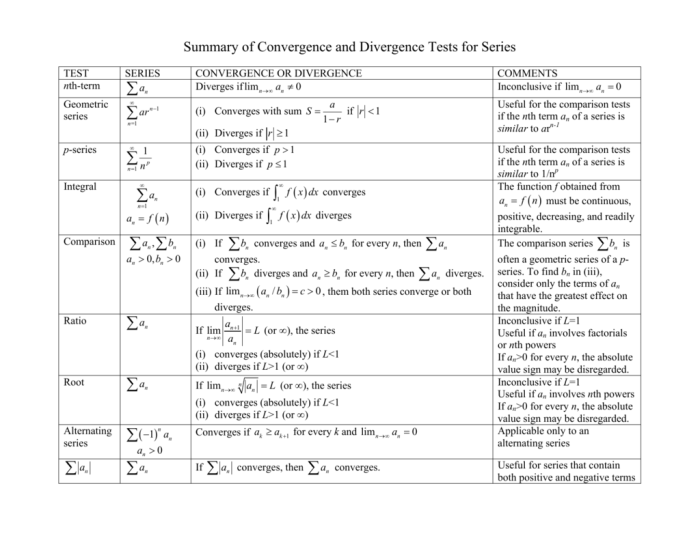
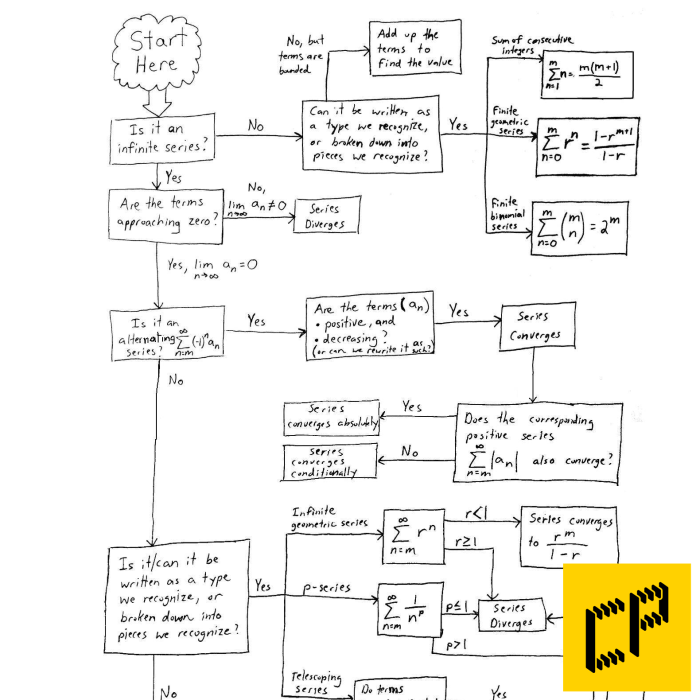
To determine whether a series converges or diverges, a comprehensive flowchart can be used. This flowchart Artikels the steps involved in applying various convergence tests, such as the ratio test, root test, and integral test.
The flowchart begins by checking if the series has non-negative terms. If so, the ratio test or root test can be applied. If the series has alternating signs, the alternating series test can be used. For series with general terms, the integral test can be employed.
By following the flowchart, one can systematically determine the convergence or divergence of a given series.
3. Applications of Series Convergence/Divergence
Series convergence and divergence have numerous applications in real-world scenarios. In calculus, they are used to evaluate improper integrals and determine the convergence of power series.
In physics, series are employed to solve differential equations and model physical phenomena such as heat transfer and wave propagation. In engineering, series are used in circuit analysis, signal processing, and control theory.
For example, in electrical engineering, the convergence of Fourier series is crucial for analyzing the frequency components of a signal.
4. Common Mistakes in Series Convergence/Divergence
Several common pitfalls and misconceptions are associated with series convergence and divergence. One common mistake is assuming that a series converges simply because its terms approach zero. However, this is not always the case, as exemplified by the harmonic series.
Another mistake is incorrectly applying convergence tests. For instance, using the ratio test for a series with alternating signs may lead to an incorrect conclusion.
To avoid these mistakes, it is crucial to understand the underlying principles of series convergence and to carefully apply the appropriate tests.
5. Advanced Topics in Series Convergence/Divergence
Beyond the basic concepts of series convergence, there are more advanced topics that delve deeper into the subject.
5.1 Absolute Convergence, Series convergence divergence flow chart
Absolute convergence refers to the convergence of a series after taking the absolute value of each term. A series that converges absolutely also converges conditionally, but not vice versa.
5.2 Conditional Convergence
Conditional convergence occurs when a series converges after rearranging its terms. However, if the terms are rearranged in a different order, the series may diverge.
5.3 Uniform Convergence
Uniform convergence refers to the convergence of a series of functions where the limit function is continuous. Uniform convergence is stronger than pointwise convergence.
These advanced topics provide a deeper understanding of series convergence and have applications in various areas of mathematics and its applications.
Clarifying Questions
What is the purpose of the Series Convergence/Divergence Flow Chart?
The Series Convergence/Divergence Flow Chart provides a step-by-step process to determine whether a given series converges or diverges, ensuring accuracy and consistency in your analysis.
How does the Flow Chart assist in understanding series convergence?
The Flow Chart simplifies the process of applying convergence tests, such as the ratio test, root test, and integral test, guiding you through the decision-making process based on the specific characteristics of the series.
What are some common mistakes to avoid when using the Flow Chart?
It is important to correctly identify the type of series (e.g., alternating series, geometric series) and carefully apply the appropriate convergence test. Avoid relying solely on the Flow Chart without understanding the underlying principles of convergence.
